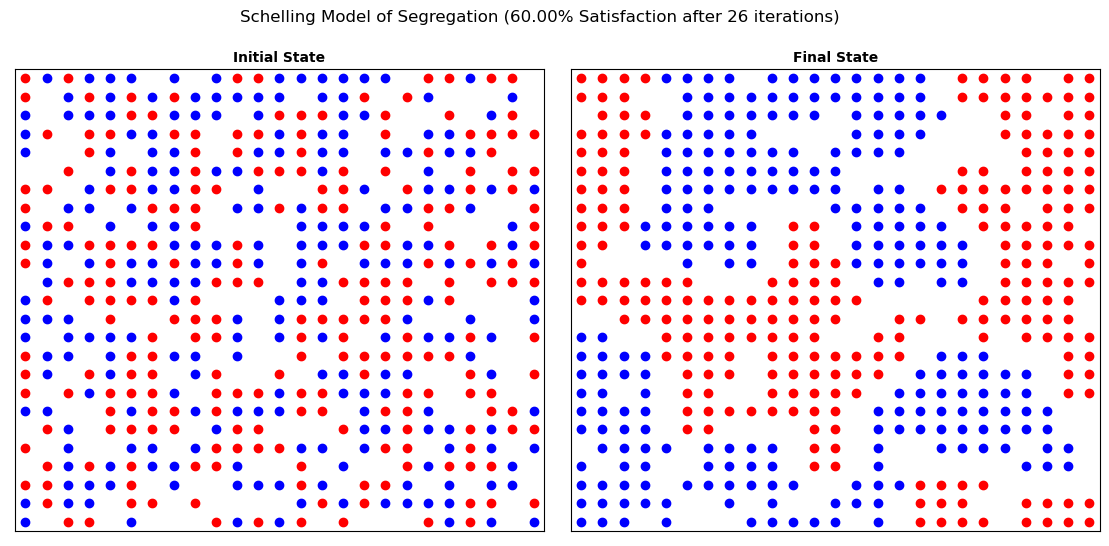
Note that this is a stochastic model, so your result will be different from mine, and different each time you run your model. unles you set the seed to 1824
"""
Understanding GIS: Practical 10
@author jonnyhuck
Schelling's segregation ABM
References:
https://github.com/adilmoujahid/schelling_simulations
http://adilmoujahid.com/posts/2014/09/schelling-model/
http://www.geog.leeds.ac.uk/courses/other/crime/abm/general-modelling/index.html
https://doi.org/10.1080/0022250X.1971.9989794
http://links.jstor.org/sici?sici=0002-8282%28196905%2959%3A2%3C488%3AMOS%3E2.0.CO%3B2-S
https://natureofcode.com/book/
New Topics:
Creating Classes
"""
from copy import deepcopy
from random import shuffle, choice, seed
from matplotlib.pyplot import subplots, savefig, subplots_adjust
class Schelling:
"""
* Class representing Schelling Model
"""
# class variable containing list of neighbours
neighbours = [ (i, j) for i in range(-1, 2) for j in range(-1, 2) if (i, j) != (0, 0) ]
def __init__(self, width, height, empty_ratio, similarity_threshold, n_iterations):
"""
* Initialise and populate the model
"""
# initialise instance variables with the arguments
self.width = width
self.height = height
self.empty_ratio = empty_ratio
self.similarity_threshold = similarity_threshold
self.n_iterations = n_iterations
# # initialise other variables
self.agents = {}
# get all house addresses
all_houses = [(x, y) for x in range(self.width) for y in range(self.height)]
# shuffle the order of the houses
shuffle(all_houses)
# calculate the number that should be empty
n_empty = int(self.empty_ratio * len(all_houses))
# identify the empty houses with list slicing
self.empty_houses = all_houses[:n_empty] # from the start to index=n_empty
# get the rest of the houses
remaining_houses = all_houses[n_empty:] # from index=n_empty to the end
# get the agents for each group using list slicing and comprehension
red_group = [[coords, 'red'] for coords in remaining_houses[0::2]] # every other cell from 0 to the end
blue_group = [[coords, 'blue'] for coords in remaining_houses[1::2]] # every other cell from 1 to the end
# add the both sets of agents to the instance variable
self.agents.update(dict(red_group + blue_group))
def is_unsatisfied(self, agent):
"""
* Determine if a particular agent is unsatisfied (too many neighbours
* from the other group)
"""
# initialise count variables
count_similar = 0
count_different = 0
# loop through neighbours
for n in self.neighbours:
try:
# log whether the group of the neighbour matches the agent
if self.agents[(agent[0]+n[0], agent[1]+n[1])] == self.agents[agent]:
count_similar += 1
else:
count_different += 1
# if we go off the edge of the map or house is empty
except KeyError:
continue
try:
# return whether or not the proportion of similar neighbours meets the threshold
return count_similar / (count_similar + count_different) < self.similarity_threshold
# catch the situation when there are only empty neighbours
except ZeroDivisionError:
# if this is the case they will be satisfied
return False
def run(self):
"""
* run the model
"""
# for each iteration (1:n, rather than 0:n-1)
for i in range(1, self.n_iterations+1):
# create a new copy of the agents
self.old_agents = deepcopy(self.agents) # note deep copy so that we can edit the elements in the collection
# init counter variable for the number of changes
n_changes = 0
# loop through each agent
for agent in self.old_agents:
# check if they are satisfied
if self.is_unsatisfied(agent):
# randomly choose an empty house for them to move to
empty_house = choice(self.empty_houses)
# add the new / remove the old location of the agent's house
self.agents[empty_house] = self.agents[agent]
del self.agents[agent]
# add the new / remove the old house from the list of empty houses
self.empty_houses.append(agent)
self.empty_houses.remove(empty_house)
# increment changes counter
n_changes += 1
# update the user
print(f"Iteration: {i}, Number of changes: {n_changes}")
# self.plot(f"Schelling Model ({i} Iterations)", f"./out/10-{i}.png")
# stop iterating if no changes happened
if n_changes == 0:
print(f"\nFound optimal solution at {i} iterations\n")
break
# if we did not find an optimal solution
if (i == self.n_iterations):
print(f"\nOptimal solution not found after {self.n_iterations} iterations\n")
# return the number of iterations
return i
def plot(self, my_ax, title):
"""
* Plot the current state of the model
"""
my_ax.set_title(title, fontsize=10, fontweight='bold')
my_ax.set_xlim([0, self.width])
my_ax.set_ylim([0, self.height])
my_ax.set_xticks([])
my_ax.set_yticks([])
# plot agents one by one
for agent in self.agents:
# we can use the agent's group name as the colour directly!
my_ax.scatter(agent[0]+0.5, agent[1]+0.5, color=self.agents[agent])
# set the seed for the analysis
seed(1824)
# setup the agents in the model
schelling = Schelling(25, 25, 0.25, 0.6, 500)
# initialise plot with two subplots (1 row, 2 columns)
fig, my_axs = subplots(1, 2, figsize=(14, 6), wspace=0.1)
# reduce the gap between the subplots
subplots_adjust(wspace=0.1)
# plot the initial state of the model into the first axis
schelling.plot(my_axs[0], 'Initial State')
# set the agents going
iterations = schelling.run()
# add the overall title into the model
fig.suptitle(f"Schelling Model of Segregation ({schelling.similarity_threshold * 100:.2f}% Satisfaction after {iterations} iterations)")
# plot the result into the second axis
schelling.plot(my_axs[1], "Final State")
# output image
savefig(f"./out/10.png", bbox_inches='tight')
print("done")