In which we further examine the impact of our projection choices upon the maps that we make.

This week, we are going to have a go at defining the level of distortion in a map. As we all now know, map distortion is a major issue, but is something that is overlooked by most GIS users.

Assessing Map Distortion

One of the reasons that people do not tend to calculate the level of distortion in a map is that there is not a very clear consensus on how this should be achieved. To resolve this, I have collected together a set of metrics from two publications:

1. Canters et al. (2005)

2. Gosling & Symeonakis (2020)

Note: You will likely need to log in to access both of these papers!

Canters et al. (2005) is all about the design of orthophanic world maps (i.e. compromise projections in which features look as expected, but none of area, shape or distance are perfectly maintained). This contains information on area and shape distortion (as these are the key distortions that affect the extent to which a map might be considered orthophanic).

Take a look at the Defining a Suitable Measure of Distortion section in Canters et al. (2005) (pages 2-5)

Gosling & Symeonakis (2020), on the other hand, is a paper that presents a method for automated map projection selection for GIS, and contains (amongst others) a measure for assessing distance distortion.

Take a look at the Distortion Assessment section in Gosling & Symeonakis (2020) (pages 267-268)

Don’t panic if you don’t understand it all, the important thing is just that you have a reasonable idea of what is going on!

A clear set of measures

Based on these two papers, we can extract metrics for all three types of map distortion:

• \(E_P\) (Ep): Distance Distortion (Gosling & Symeonakis (2020))
• \(E_S\) (Es): Shape Distortion (Canters et al. (2005))
• \(E_A\) (Ea): Areal Distortion (Canters et al. (2005))

In order to make the areal distortion a little easier to understand, we are also going to add a fourth measure, \(K_A\)which is calculated from \(E_A\), and gives a much more meaningful impression of the extent of areal distortion.

• \(K_A\)(Ka): Scale Factor (Canters et al. (2005))

Based upon these measures, we can clearly define the extent of each type of distortion for a given map, which is an extremely desirable thing to do, especially when we are trying to decide which CRS we should use to present and/or analyse our data!

Note: this week, we will break with convention and not use snake_case in some cases, in order to match variable names to the mathematical notation above. This is not unusual in mathematical applications of Python.

Getting Setup

Defining the map

For this exercise, we will focus on a map of a single country. We will start with Greenland, as this is a country at a very high latitude, and so is famously badly affected by distortion, as you can see if you drag it around in the below map (which uses the Web Mercator projection):

Open the "../data/natural-earth/ne_10m_admin_0_countries.shp" file as a GeoDataFrame and load it into a variable called world. Remember to add the necessary import statement at the top of your code.

Extract the Greenland row from the GeoDataFrame (world.ISO_A3 == GRL) and store it in a variable called country.

We need to begin by extracting the bounds of Greenland. We will do this using the .total_bounds property of the GeodataFrame. This is useful, as it accounts for the bounds of all parts of the country (which is useful for countries that are made up of multiple components, such as the UK as we saw last week).

Add the below snippet to calculate the bounds of Greenland, and use variable expansion to extract them into 4 separate variables (rather than a Tuple of 4 items)

# get the bounds of the country
minx, miny, maxx, maxy = country.total_bounds

Add a print() statement to test the bounds, if all has gone to plan they should look something like this:

-73.05724036399994 59.792629299000055 -11.37682044199994 83.63410065300008

Defining our Geodesic model and CRSs

Fundamentally, each of the three measures (\(E_P\), \(E_S\), \(E_A\)) are calculated by simply comparing a measure of each property (distance, shape, area) taken using a circle drawn on the ellipsoid, to one drawn using the selected projection. The closer that each projected circle is to the ellipsoidal version, the less distortion there is, and vice-versa. Simple!

For the purposes of this research, we will use the WGS84 Datum (referencing the WGS84 ellipsoid model), which is a pretty solid choice for working at a global scale (it is the one that the GPS uses). As we saw in Week 3, if we were limiting our analysis to a specific region, then we might want to look for a Local Datum (e.g., Arc 1960 for East Africa, which references the Clarke 1880 ellipsoid). Let’s get started then:

Initialise a pyproj Geod object set to WGS84 with the below snippet (remember to add the necessary import statement at the top of your code):

# set which ellipsoid you would like to use
g = Geod(ellps='WGS84')

Now we need to define the two CRSs that we will be comparing: we need one that is geographical (3D coordinates measured in longitude and latitude), and one that is projected (2D planar coordinates measured in metres):

• As with the Geodesic model that we have set above, we will use WGS84 for our geographical CRS which you can look up here.

• To start with, we will use a well-known Equal Area projection called Eckert IV for our projected CRS, which you can look up here.

Get the Proj4 strings for both CRSs and store them in variables called proj_string (Eckert IV), and geo_string (WGS84)

Now that we have defined our two CRSs, we need to create a pyproj.Transformer object, which enables you to transform coordinates from one CRS to the other, and vice-versa.

Edit your import statements so that you are importing CRS and Transformer from pyproj

Add the below snippet to create a Transformer object that can transform coordinates between your two CRSs:

# initialise a PyProj Transformer to transform coordinates
transformer = Transformer.from_crs(CRS.from_proj4(geo_string), CRS.from_proj4(proj_string), always_xy=True)

Note how this takes in two pyproj.CRS objects to define the transformation, and also that we need to force it to use coordinates in the order Longitude-Latitude (x, y). This is because some people (e.g. Google Maps) prefer to do things in the order Latitude-Longitude, but I can’t see any justification for this at all - and it can easily lead to many errors if you get them mixed up - so I always try to stick with the conventional x-y (Longitude-Latitude) approach!

Calculating Areal and Shape Distortion

Now we have all of our setup out of the way, we can start actually calculating our distortion metrics.

Create a def statement to add a function to your code as per the below instructions - remember that functions go below the import statements, but above the main code

• The function should be called evaluate_distortion
• It should take in 7 arguments: g, transformer, minx, miny, maxx, maxy and sample_number
• It should return 4 values, one for each measure (\(E_P\), \(E_S\), \(E_A\), \(K_A\)). For now, just set the return statement to return 0, 0, 0, 0. This is temporary measure just until we have completed the function!

Now, add a call to that function as per the below snippet (think about where this should go- not inside the function!!). This function call is so the function actually runs when we execute the code (rather than just being created), which allows us to run tests on our progress as we write.

# calculate the distortion
Ep, Es, Ea, Ka = evaluate_distortion(g, transformer, minx, miny, maxx, maxy, 1000)

This statement passes our transformer object and map bounds as arguments, along with the number 1000, which describes how many samples we want to take as part of our calculations. We need to define a number of samples because these measures all assess distortion at a particular point in space, not across the whole map. In order to get an impression of the level of distortion across all maps, we will need to take many measurements. We will achieve this by taking 1,000 random locations, and combining results from all of these points to get our final value (hence passing 1000 as the 6^th argument above).

Note: Until we get to the return statement, the majority of the up-coming code should be placed inside the evaluate_distortion function, unless otherwise specified!

Random Sampling

In order to assess distortion across the whole map, we will draw 1,000 circles of randomly selected size at randomly selected locations. In order to select 1,000 random locations within the study area, we need to do nothing more complicated than selecting 1,000 random x coordinates (longitude) and 1,000 random y coordinates (latitude); each within the bounds that we defined earlier. We will then draw a circle (with a random radius) at each of these 1,000 locations.

We will achieve this using numpy, which (as the name suggests) is a maths package for Python. numpy contains many functions to help us create sets of random numbers - we will use one called uniform(), which draws random numbers from a uniform distribution. This sounds a bit complicated, but simply means that all numbers between the supplied bounds are equally likely to be returned. This as opposed to a normal distribution, for example, where numbers near the middle of the range would be more likely to be returned than those near the bounds. Because we want a relatively even coverage of points across our whole area, uniform() is the choice for us!

Here is how to collect our random x locations:

from numpy.random import uniform

# calculate the required number of random locations (x and y separately) plus radius
xs = uniform(low=minx, high=maxx, size=sample_number)

This will return a list with a length equal to size, in which each element is a random number between low and high. Here you can see that we are using keyword arguments, where each argument is named (you have seen these before in the .plot() function, for example). These are exactly the same as normal arguments, they are just convenient for when a function has a lot of optional arguments, as it means that you only have to specify values for the arguments that you are interested in, and can accept the default values for the others.

Add the above snippets to your code (the import at the top and the function call in your evaluate_distortion() function), then add two more lines to get the random ys (latitudes, based on the bounds) and rs (random circle radii, ranging from 1000 to 1000000)

Print some values from your resulting lists to see if they are as expected

In order to construct our circles, we will use the approach described by Canters et al. (2005):

For each [circle] 16 positions along its perimeter are calculated, corresponding to
azimuthal angles of 0,22.5,45,..., defined from the centre of the circle. By 
projecting each position along the circle's outline in the plane a polygon with 16
vertices is obtained.

In order to achieve this, we will need to prepare a list of azimuths (directions) in which the centre point will need to be offset in order to construct our circle.

Add the below snippets to your code in order to define your 16 directions using arange() (very similar to the already familiar range()) - here we are achieving this by asking for a list of numbers from 0-360 at intervals of 22.5 (¹/₁₆ of a circle)

from numpy import arange

# offset distances
forward_azimuths = arange(0, 360, 22.5)
n = len(forward_azimuths)

We will not actually construct our circles just yet - but now we have prepared everything that we need to do so. We have also recorded the number of azimuths in our list (n), which will be handy later on.

Looping through our random circles

Now that we have everything in place for our random circles, we need to loop through the random data that we have created. As we have three lists that we want to loop through (xs, ys, rs), we are going to use the zip() function in Python to allow us to loop through them all at once.

zip is used to join lists together into a single multidimensional list (a list of lists). For example:

# create two lists
list_1 = [1, 2, 3, 4, 5]
list_2 = ['A', 'B', 'C', 'D', 'E']

# zip and extract using variable expansion
for x, y in zip(list_1, list_2)
	print(x, y)

…which would return:

1 A
2 B
3 C
4 D
5 E

make sure that you understand zip() - if you need a little more info, you can get it here.

In our case, we want to join our 3 lists and loop through them all, which we can do using:

# loop through the points
planar_areas = []
shape_indices = []
ellipsoidal_areas = []
for x, y, r in zip(xs, ys, rs):

Now each random circle is defined by x, y and r in each iteration of the loop - great! We will initialise some empty lists while we’re at it to store various properties of each circle.

Add the above snippet to your code

Building our random circles

In order to assess our circles, we need to construct the same circle twice, using two slightly different approaches:

• construct a circle using geographical coordinates and then transform it to projected coordinates
• construct the same circle, but this time using projected coordinates

We then assess the level of distortion in the map by comparing these circles.

Here is how we do it:

Step 1: we can construct our circle by simply offsetting our point along the ellipsoid by a given distance and direction (forward azimuth). As you might remember from Week 2, we have an equation that will do this for us called the Forward Vincenty Equation, and that is available to us thanks to pyproj as g.fwd():

# construct a circle around the centre point on the ellipsoid
lons, lats = g.fwd([x]*n, [y]*n, forward_azimuths, [r]*n)[:2]

As with the g.inv() function that you will remember from Week 2, g.fwd() returns three sets of values (one or more longitudes, one or more latitudes and the back azimuth). Because we are not interested in the back azimuth, we can ignore it using list slicing, where we extract only the first two elements from the returned collection using [:2].

Unlike the example from Week 2, here we are passing in lists as each of the arguments (rather than single values). This is a convenient feature of the g.fwd() function, which means that it can either take in single values as arguments (and return single values), or lists as arguments (and return lists). The only snag here is that we only have one list (forward_azimuths), as x, y and r all remain the same. Fortunately, Python has a simple solution for us - we can put the single value in a list (by surrounding it with square brackets), and then multiply that our desired length, which will duplicate the one value as many times as we multiply by:

bunch_of_fives = [5]*10
print(bunch_of_fives)

…which gives:

[5, 5, 5, 5, 5, 5, 5, 5, 5, 5]

Handy!

Make sure that you fully understand the g.fwd() statement and then add it to your loop

Next, we want to loop through our lists of ellipsoidal coordinates (lons and lats) and project them, which we simply do by passing to transformer.transform(). For convenience we will use List Comprehension to do this in a single line. We will then store the area of this circle (which we calculate by building the coordinates into a shapely Polygon and then using the .area property).

Note that direction='FORWARD' refers to the fact that we are transforming from geographical to projected coordinates. direction='BACKWARD' would be from projected to geographical.

from shapely.geometry import Polygon

# project the result, calculate area, append to the list
e_coords = [ transformer.transform(lon, lat, direction='FORWARD') for lon, lat in zip(lons, lats)]
ellipsoidal_areas.append(Polygon(e_coords).area)

Add the above snippet to your code and make sure that you understand it

Add a print statement after your for loop to see how long the ellipsoidal_areas list is. Is this as expected? Remember to delete it after you are finished with it!

Now we have the area for our circle defined on the ellipsoid, we will do exactly the same thing for a circle calculated using projected coordinates. To do this, we simply need to transform the x, y coordinate, and then calculate the offsets using planar geometry (simple trigonometry) rather than the Forward Vincenty Equation. You can read more about how this works on my Trigonometry page.

To achieve this add the below three snippets to your code at the appropriate locations (think about where import statement and functions go - these should not be inside evaluate_distorion()!):

from math import sin, cos, radians

def offset(x, y, distance, direction):
    """
    * Offset a location by a given distance and direction
    """
    x2 = x + cos(radians(direction)) * distance
    y2 = y + sin(radians(direction)) * distance
    return (x2, y2)

# transform the centre point to the projected CRS
px, py = transformer.transform(x, y, direction='FORWARD')

# construct a circle around the projected point on a plane, calculate area, append to list
p_coords = [ offset(px, py, r, az) for az in forward_azimuths ]
planar_areas.append(Polygon(p_coords).area)

Add another temporary print() statement to check the length of planar_areas - is this also as expected?

Next, we will calculate the radial distances for each of our sets of random circles, in order to compare them.

To measure distance in projected data, we simply need to use Pythagoras’ Theorem, just as we did in Weeks 3 and 4. However, in this case, we will make use of a convenience function in the Python math library called hypot, which returns the length of the hypotenuse of a triangle if you give it the other two sides (instead of using your own implementation like you have done previously).

Edit your import statements to import hypot from the math library

Now we have our measurement function, it is simply a matter of looping through each coordinate pair and measuring the distance from the centre point. This is based on the simple principle that, if there is no shape distortion, then the distance to each of them will be the same. If, however, there is distortion, then there will be some variation, and so testing for this variation allows us to see how much distortion there is.

Note that we are only doing this on the coordinates that we constructed on the ellipsoid and then projected - obviously the coordinates that we constructed on the planar surface will all be the same distance away!

Once we have this, we get the sum of these distances (using sum()) and the expected distance of each one (the total distance divided by the number of points).

# get radial distances from the centre to each of the 16 points on the circle
ellipsoidal_radial_distances = [ hypot(px - ex, py - ey) for ex, ey in e_coords ]

# get the sum of the distances, and the expected value for each distance
total_radial_dist = sum(ellipsoidal_radial_distances)
expected_distance = total_radial_dist / n

Make sure that you understand what the above snippet is doing, and then add it to your code

Now, all that remains is to loop through the ellipsoidal_radial_distances and calculate the shape distortion, which is described by Canters et al. (2005) in their paper as:

...the proportion of each radial distance with respect to the sum of all 16 distances
is calculated and subtracted from the proportion each radial distance would represent 
if the circular shape would have been retained (1/16)

This translates to the following:

# get the difference between the actual and expected radial distance for each 'spoke'
shape_distortion = [ abs((expected_distance / total_radial_dist) - (d / total_radial_dist)) for d in ellipsoidal_radial_distances ]
shape_indices.append(sum(shape_distortion))

Note the use of the abs() function, which refers to absolute number. This simply means that negative numbers become positive (i.e., you should ignore any negative signs, e.g., abs(-2) would be 2, whereas abs(3) would remain 3).

Make sure that the above makes sense, and add it to your loop

Add a temporary print() statement to make sure that you have the number of values that you would expect (one per circle…)

Now we should have everything that we need, we can calculate our first two indices!

According to Canters et al. (2005), for \(E_S\) this is simply a matter of averaging our shape_indices values once the loop has completed.

Work out the average of the values in shape_indices and store it in a variable called Es

If all has gone to plan, this should be something in the region of 0.314 (it won’t be exactly the same, as we are using a random sample!)

Check that your value is as expected with a temporary print() statement.

Next, we can calculate our areal distortion, which is defined by Canters et al. (2005) as:

where:

• \(m\) is the sample size
• \(S_i\) is the ellipsoidal area of a circle
• \(S'_i\) is the projected area of a circle

For the non-mathematicians amongst you, it is also useful to know that:

• \(\sum_{i=0}^m\) means “sum of all of the values from 0 to \(m\)”
• Putting an expression within pipe symbols ( |…| ) means absolute number - this is simply saying that you should ignore any negative signs (so make all numbers positive, e.g. -2 would become 2). As we saw above, this is done in Python using the abs() function

This translates to:

# get the sum of the differences between the ellipsoidal and planar circle areas
diff_sum = 0
for e, p in zip(ellipsoidal_areas, planar_areas):
  diff_sum += abs(e - p) / abs(e + p)

# calculate the Ea and Ka numbers
Ea = 1 / sample_number * diff_sum

Canters et al. (2005) also explains how to calculate the scale factor (\(K_A\)) from the \(E_A\), which is much more meaningful to interpret.

Get the equation for \(K_A\) from Canters et al. (2005) (don’t worry, it isn’t a scary one) and calculate the scale factor for your map. Store the result in a variable called Ka

print() your values for \(E_A\) and \(K_A\)

If all has gone to plan, you should have something like the below (remember - it is OK if they are not exactly the same, as we are using random samples!):

Ea: 0.004
Ka: 1.007

Give yourself a pat on the back, that was a bit complicated…!

Calculating Distance Distortion

OK, we have now calculated 3 of our 4 metrics - only one to go!

The Distance Distortion metric comes from Gosling & Symeonakis (2020), where it is presented alongside an alternative areal distortion measure (which we are not using). Conveniently, this metric for distance distortion is pretty much exactly the same as the one that we have used for area!

The only difference is that in this case, \(S_i\) and \(S'_i\) in this case refer to the measured distance between a pair of random points (ellipsoidal and projected respectively), as opposed to the area of a randomly generated circle.

As you might imagine, the process is also quite similar, lets get started:

Initialise two empty lists called ellipsoidal_distances and planar_distances.

Use range() to make a for loop that will run sample_number times

Inside the loop, use two calls to uniform() to generate two random locations within the map bounds. Store the resulting coordinates in variables called xs and ys

Add a temporary print() statement to make sure that you are getting coordinates as expected

We now need to calculate the distance between the two locations across the ellipsoid. Ordinarily, we would expect to use the g.inv() function to do this, just like we did in Week 2. This time, however, we are going to use the g.line_length() function, which does pretty much the same thing - the only differences are that it does not also return the forward and back azimuths (which we do not need) as well as the distance, and it takes the coordinates as two arrays (one of x coordinates, one of y coordinates), which is the format in which we already have the coordinates (xs & ys).

Here is how it works:

# calculate the distance along the ellipsoid
ellipsoidal_distances.append(g.line_length(xs, ys))

Add the above snippet to your loop to calculate the distance and append it to the relevant list

Add a temporary print() statement to make sure that the results are expected

Next, we need to undertake the same measurement exercise for the projected points:

Add two transformer.transform() statements to project both of your random locations. Store the results in two variables called origin and destination

Calculate the distance between the two points using hypot() (as you did earlier) and append the result to planar_distances

That is all that we need for our loop, you are now ready to calculate your metric!

Outside of the loop, calculate \(E_P\) (remember, it is exactly the same equation as \(E_A\)!)

Finally…

Modify the return statement for evaluate_distortion() so that it returns Ep, Es, Ea, Ka in that order (instead of 0, 0, 0, 0)

Note: Now we have updates the return statement, our evaluate_distortion() function is complete - we can return to working in the main body of code now (i.e., outside the function block).

Immediately after the function call to evaluate_distortion() (not inside the function!!), add the following snippet to check your results:

# report to user
print(f"Distance distortion\t(Ep): {Ep:.3f}")
print(f"Shape distortion\t(Es): {Es:.3f}")
print(f"Area distortion\t\t(Ea): {Ea:.3f}")
print(f"Scale factor\t\t(Ka): {Ka:.3f}")

Are the results as expected for an equal area map?

You should expect to see something in the region of (but not exactly):

Distance distortion     (Ep): 0.201
Shape distortion        (Es): 0.314
Area distortion         (Ea): 0.004
Scale factor            (Ka): 1.007

Note how we have inserted tab characters (\t)into our strings to give the output a neat, table-line appearance!

Shape and distance have been changed, but area is almost exactly as expected. However, almost exactly as expected might not be good enough for our purposes! You can read more about this problem in equal-area map projections in the article: All Equal-Area Map Projections Are Created Equal, But Some Are More Equal Than Others by Usery and Seong (2001).

Making a map

Now we have our results, all that remains is to convert them into a lovely map! In this case, I would like you to draw your chosen country and add one pair of circles (one defined on the ellipsoid and projected; one defined using the projection), which will act as a visual illustration of the patterns of distortion.

To do the next step, you will need to work out how to work out the centre point of map, which is quite straightforward using this equation (simply swap \(x\) for \(y\) to get the \(y\) coordinate):

Alternatively, simply taking the average of the two coordinates should give the same result!

Create 3 variables: x_centre, y_centre and radius. Set the value of x_centre and y_centre to the coordinates of the centre point of the bounds of Greenland (see above) and set radius to 400000.

Now we will construct our two circles, and convert them into GeoDataFrames to allow us to add them to the map. This time we will use 60 points (rather than 12) to construct the ellipsoidal one (to give us a nice, smooth circle), and we can use the shapely .buffer() function to make the projected one.

Add the below snippets to create your two circles and convert them to GeoDataFrames (note that both of the import statements can be combined with existing ones)

from shapely.geometry import Point
from geopandas import GeoSeries

# draw a circle on the ellipse and add make a GeoSeries
lons, lats = g.fwd([x_centre]*60, [y_centre]*60, list(range(0, 360, 6)), [radius]*60)[:2]
circle1 = Polygon([ transformer.transform(lon, lat, direction='FORWARD') for lon, lat in zip(lons, lats) ])
circle_1 = GeoSeries(circle1, crs=proj_string)

# draw a circle on the plane and add make a GeoSeries
x_centre, y_centre = transformer.transform(x_centre, y_centre, direction='FORWARD')
circle2 = Point(x_centre, y_centre).buffer(radius)
circle_2 = GeoSeries(circle2, crs=proj_string)

Now, plot the map with the below snippets:

from matplotlib.patches import Patch
from matplotlib.pyplot import subplots, savefig
from matplotlib_scalebar.scalebar import ScaleBar

# create map axis object
fig, my_ax = subplots(1, 1, figsize=(16, 10))
my_ax.axis('off')

# set title
my_ax.set_title(f"Distortion Analysis:\nEp: {Ep:.3f}; Es: {Es:.3f}; Ea: {Ea:.3f}; Ka: {Ka:.3f}")

# plot country
country.to_crs(proj_string).plot(
    ax = my_ax,
    color = '#ffffff',
    edgecolor = '#000000',
    linewidth = 0.5,
    )

# plot geographical circle
circle_1.plot(
    ax = my_ax,
    color = '#f0e0e0',
    alpha = 0.5,
    edgecolor = '#660000',
    linewidth = 0.5,
    )

# plot planar circle
circle_2.plot(
    ax = my_ax,
    color = '#e0e0f0',
    alpha = 0.5,
    edgecolor = '#000066',
    linewidth = 0.5,
    )

# manually draw a legend
my_ax.legend([
    Patch(facecolor='#f0e0e0', edgecolor='#660000', label='Ellipse'),
    Patch(facecolor='#e0e0f0', edgecolor='#000066', label='Projected')],
	['Ellipse', 'Projected'], loc='lower left')

# add scalebar
my_ax.add_artist(ScaleBar(dx=1, units="m", location="lower right"))

# add north arrow
x, y, arrow_length = 0.99, 0.99, 0.1
my_ax.annotate('N', xy=(x, y), xytext=(x, y-arrow_length),
	arrowprops=dict(facecolor='black', width=5, headwidth=15),
	ha='center', va='center', fontsize=20, xycoords=my_ax.transAxes)

# save the result
savefig('out/5.png', bbox_inches='tight')
print("done!")

Switch your chosen projection (proj_string) to Web Mercator (which, as it has “Mercator” in the title, we will assume is Conformal) and re-run the code.

You should now get something like the below:

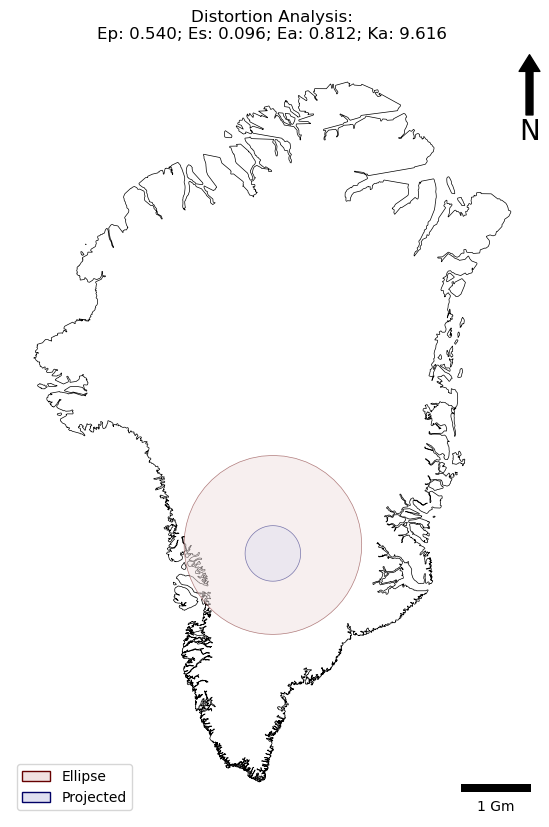
Distance distortion     (Ep): 0.540
Shape distortion        (Es): 0.096
Area distortion         (Ea): 0.812
Scale factor            (Ka): 9.616

This time, area (\(E_A\)) and distance (\(E_P\)) are way off - the scale factor shows that Greenland is almost 10x too big!! Critically, it also shows that the shape Distortion (\(E_S\)) is 0.096 (and the red polygon is not a perfect circle) meaning that the Web Mercator Projection is NOT Conformal! You can read more about this in Battersby et al (2014), and on the Wikipedia page.

Compare the values of the 4 metrics, and the appearance of Greenland on both of your outputs. Are they as expected?

Now try a few different countries and see how the metrics change at different latitudes

And there you have it - you now know how to assess the distortion on a map!

Have a think about how neither of these widely-used map projections do exactly what we expected them to do, then reflect on the way that you select map projections in your other modules. This is why this kind of understanding is so valuable - as you now have the power to actually check!!!

Making your code into a library

The last thing that we will do this week is to convert our code so that we can call it as a library from another Python Script. This is surprisingly easy to do, all that you need is to take the code that is not inside a function and put it inside the following if statement:

if __name__ == "__main__":
  # code goes here

That will give you the following structure:

# imports 

# functions

if __name__ == "__main__":
	# rest of your code

Though a little ugly, this statement is very useful because it means that the code inside its block will only be executed if the script is being run directly, whereas it will be ignored if it is called by another program. This works because the Python interpreter sets a ‘special’ variable called __name__ to equal __main__ in the script that is executed, meaning that the result of if __name__ == "__main__": will be True in the script that was executed, but False in any external scripts that are that are accessed via import statements.

Add a if __name__ == "__main__": statement to your code so that nothing will happens if it is imported.

Add a new file called test.py to your week5 directory and add the following. Save and run to test it. If it works you should get the a similar answer (accounting for the randomness) as you got from your other script (make sure that the countries are the same, of course…)!

from geopandas import read_file
from week5 import evaluate_distortion
from pyproj import Geod, CRS, Transformer

# set the projected CRS' to evaluate for distortion
proj_string = "+proj=eck4 +lon_0=0 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs"  # Eckert IV (Equal Area)

# set the geographical proj string and ellipsoid (should be the same)
geo_string = "+proj=longlat +datum=WGS84 +no_defs"
g = Geod(ellps='WGS84')

# load the shapefile of countries and extract country of interest
world = read_file("../data/natural-earth/ne_10m_admin_0_countries.shp")

# set country using country code
country = world.loc[world.ISO_A3 == "GRL"]

# get the bounds of the country
minx, miny, maxx, maxy = country.total_bounds

# initialise a PyProj Transformer to transform coordinates
transformer = Transformer.from_crs(CRS.from_proj4(geo_string), CRS.from_proj4(proj_string), always_xy=True)

# calculate the distortion
Ep, Es, Ea, Ka = evaluate_distortion(g, transformer, minx, miny, maxx, maxy, 1000)

# report to user
print(f"Distance distortion\t(Ep): {Ep:.6f}")
print(f"Shape distortion\t(Es): {Es:.6f}")
print(f"Area distortion\t\t(Ea): {Ea:.6f}")
print(f"Scale factor\t\t(Ka): {Ka:.6f}")

Now you can import that functionality into your script any time you like, simply copy the week4.py file into your working directory and use it as above!

We have done this because these functions are not included in any mainstream GIS systems or Python libraries, so it will be very useful for you to be able to uses these to evaluate the level of distortion in your future maps!

A little more…

If you want to keep going, see if you can implement the alternative area metric (\(r\)) given by Gosling & Symeonakis (2020) (equation 3, page 268). This is simply done by creating the polygons of the two versions of your circle (which you already do) and then using the .intersection() and .union() topological operators from shapely (see Week 2 or the Handy Hints page)

where:

• \(K\) = The circle created on the ellipsoid and then projected (\(S\) in the above)
• \(L\) = The circle created using a projection (\(S'\) in the above)
• \(\cap\) intersect (it looks like an n for intersection)
• \(\cup\) union (it looks like a u for union)
• (\(K \cap L\) would therefore be: the area of the polygon created by an intersection between polygon \(K\) and polygon \(L\))

As with the shape distortion metric, you would calculate \(r\) for each circle in your random sample, and then get the mean value to give you the overall \(r\) value.

How does it compare to the \(E_A\) areal distortion metric presented by Canters et al. (2005)?