"""
Understanding GIS: Practical 9
@author jonnyhuck
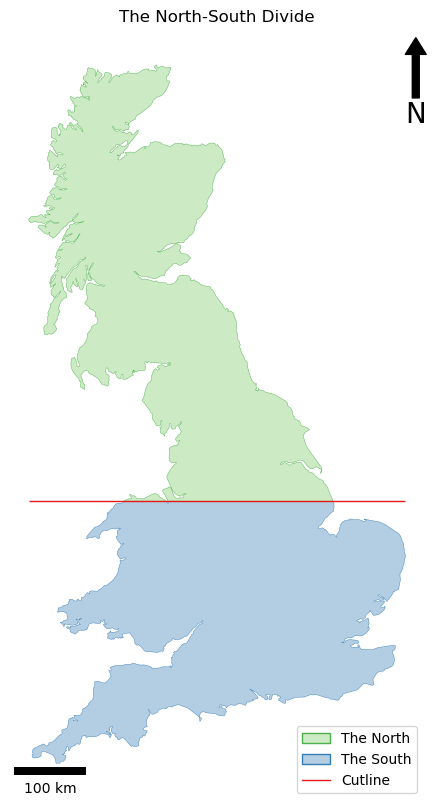
Resolve the North-South divide using a Genetic Algorithm
References:
https://projectionwizard.org/#
New Topics:
Lambda Functions
"""
from sys import exit
from shapely.ops import split
from fiona.errors import DriverError
from matplotlib.patches import Patch
from numpy.random import randint, uniform
from geopandas import read_file, GeoSeries
from matplotlib_scalebar.scalebar import ScaleBar
from shapely.geometry import LineString, MultiPolygon
from matplotlib.pyplot import subplots, savefig, Line2D
def group_polygons(polys, individual):
"""
Convert list of polygons into two multipolygons, grouped above and below the cutline.
"""
# loop through all polygons
top = []
bottom = []
for poly in polys.geoms:
# if the max y value, is it above the cutline, then it is part of the top 'half'
if poly.bounds[3] > individual['y']:
top.append(poly)
# otherwise, it is part of the bottom 'half'
else:
bottom.append(poly)
# return list of two multipolygons
return [MultiPolygon(top), MultiPolygon(bottom)]
def get_fitness(population):
"""
Calculate the fitness of a position on the y-axis by splitting the polygon at
the desired position on the y-aixs and comparing the area of the two resulting
polygons.
"""
# calculate fitness of each individual
for individual in population:
# split the polygon into two along the cutline
polys = group_polygons(split(gb, LineString([(gb.bounds[0], individual['y']), (gb.bounds[2], individual['y'])])), individual)
# overwrite polys with a sorted version of itself
polys = sorted(polys, key=lambda poly: poly.area)
# update fitness as ratio of smallest to largest
individual['fitness'] = polys[0].area / polys[1].area
# return the resulting array
return population
def crossover(parents, offspring_size):
"""
* Single point crossover function for decimal numbers
"""
# loop enough times to make the offspring size
offspring = []
for i in range(offspring_size):
# get binary representations of parents' y values
parent_1 = list(bin(parents[i % len(parents)]['y'])[2:])
parent_2 = list(bin(parents[(i+1) % len(parents)]['y'])[2:])
# swap some random chromasomes (bits) in the binary strings
for r in randint(len(parent_1)-1, size=len(parent_1) // 2):
parent_1[r] = parent_2[r]
# convert back to number and store in a dictionary
offspring.append({'y': int("".join(parent_1), 2), 'fitness': None})
# return the next generation
return offspring
def mutation(population, mutation_probability, max_mutation):
"""
* Mutate a value by +/- max_mutation
"""
# mutation changes a single gene in each offspring randomly.
for i in range(len(population)):
# does this child want to mutate?
if (uniform() < mutation_probability):
# apply the random value as a mutation to the child
population[i]['y'] += int(uniform(-max_mutation, max_mutation))
# return the resulting offspring
return population
# define CRS
uk_ea = '+proj=tcea +lon_0=-3 +datum=WGS84 +units=m +no_defs'
# Load the shapefile and project
try:
world = read_file('../data/natural-earth/ne_10m_admin_0_countries.shp').to_crs(uk_ea)
# if the file does not exist, warn and exit
except DriverError:
print("Warning, invalid filepath. Exiting.")
exit()
# extract the geometry of the UK
uk = world[(world.ISO_A3 == 'GBR')]['geometry'].iloc[0]
# extract the largest polygon (mainland Great Britain)
gb = sorted(uk.geoms, key=lambda poly: poly.area, reverse=True)[0]
# settings
pop_size = 50 # population size
num_parents_mating = 10 # mating pool size (how many of the pop get to breed)
threshold = 0.999 # the desired precision of the result
mutation_probability = 0.1 # probability of a child mutating
max_mutation = 100000.0 # 10km max mutation
# create the initial population (array of dictionaries) then calculate the fitness for each individual
population = [{'y': int(y), 'fitness': None} for y in uniform(low=gb.bounds[1], high=gb.bounds[3], size=pop_size)]
population = get_fitness(population)
# initialise loop varibles
generation = 0
best_fit = 0
previous_best_fit = None
# loop until we either find a solution to within the threshold, or the solutions stop improving
while best_fit < threshold and best_fit != previous_best_fit:
# select the best parents in the population for mating
parents = sorted(population, key=lambda individual: individual['fitness'], reverse=True)[:num_parents_mating]
# get the next generation, mutate and update fitness values
population = get_fitness(mutation(crossover(parents, pop_size), mutation_probability, max_mutation))
# get the current best individual
best_match = sorted(population, key=lambda individual: individual['fitness'], reverse=True)[0]
previous_best_fit = best_fit
best_fit = best_match['fitness']
# increment generation counter and report current fitness (1 = perfect)
generation += 1
print(f"\tgeneration {generation}: {best_fit}")
# report the best match and output
print(f"Best solution : {best_match['y']} (fitness: {best_match['fitness']} generations: {generation})")
# construct the final answer as a linestring
cutline = LineString([(gb.bounds[0], best_match['y']), (gb.bounds[2], best_match['y'])])
# split GB to get the two polygons
polys = group_polygons(split(gb, cutline), best_match)
# setup figure for output
fig, my_ax = subplots(1, 1, figsize=(16, 10))
my_ax.axis('off')
my_ax.set_title("The North-South Divide")
# add layers
GeoSeries(polys[0], crs=uk_ea).plot(
ax = my_ax,
color = '#ccebc5',
edgecolor = '#4daf4a',
linewidth = 0.3
)
GeoSeries(polys[1], crs=uk_ea).plot(
ax = my_ax,
color = '#b3cde3',
edgecolor = '#377eb8',
linewidth = 0.3
)
GeoSeries(cutline, crs=uk_ea).plot(
ax = my_ax,
color = '#e41a1c',
linewidth = 1
)
# manually draw a legend
my_ax.legend([
Patch(facecolor='#ccebc5', edgecolor='#4daf4a', label='The North'),
Patch(facecolor='#b3cde3', edgecolor='#377eb8', label='The South'),
Line2D([0], [0], color='#e41a1c', lw=1)],
['The North', 'The South', 'Cutline'], loc='lower right')
# add north arrow
x, y, arrow_length = 0.98, 0.99, 0.1
my_ax.annotate('N', xy=(x, y), xytext=(x, y-arrow_length),
arrowprops=dict(facecolor='black', width=5, headwidth=15),
ha='center', va='center', fontsize=20, xycoords=my_ax.transAxes)
# add scalebar
my_ax.add_artist(ScaleBar(dx=1, units="m", location="lower left"))
# store image
savefig("./out/9.png", bbox_inches='tight')
print("done!")