There are three fundamental operations that I think any GIS operator should understand (working with projected coordinates):

• Calculate the distance between two points
• Work out the heading (direction, in degrees) from one point to another
• Calculate a new point at a given distance and heading from an existing point

In fact, whenever I hired a new member of staff, the first task that I asked them to complete was to create a simple spreadsheet demonstrating that they could apply simple trigonometry to solve these three problems. It was very rare that anyone would be able to do this straight away, but actually it is quite simple - the skills required are nothing more than we learn in high school maths! Most importantly, understanding these few things gives you some great insight into the inner workings of GIS, and you can apply this understanding to solving more complex GIS challenges.

I know that this kind of stuff isn’t everyone’s cup of tea, but with a bit of effort you can get your head round this stuff- and it really does come in handy more often than you would think if you end up doing a job that involves GIS (or any type of mapping whatsoever) - I can’t tell you how many times I have used these!

Here I will explain each of them in turn:

• Distance

• Heading

• Offset

Distance

You should remember this from week 2 and week 3 that when working with projected coordinates, a distance calculation is nothing more than a straightforward application of Pythagoras’ Theorem:

where a is the length of the hypotenuse (the longest side), and b and c are the other two sides of a right-angled triangle. For for a distance calculation, therefore, this could be better described as:

where \(\Delta\) (delta) means difference (so \(\Delta x\) would be the difference in the x coordinates).

Handily, the Python math library has a convenience function built into it called hypot that calculates the length of the hypotenuse if you give it \(\Delta x\) and \(\Delta y\) as arguments:

from math import hypot

def compute_distance(location1, location2):
    return hypot(location1[0] - location2[0], location1[1] - location2[1])

If you don’t want to use the built in function, you can calculate it yourself using the sqrt()and pow() functions instead:

from math import sqrt, pow

def compute_distance(location1, location2):
	return sqrt(pow(location1[0] - location2[0],2) + pow(location1[1] - location2[1],2))`

Or you can even do it without any imported functions whatsoever:

def compute_distance(location1, location2):
	return ((location1[0] - location2[0])**2 + (location1[1] - location2[1])**2)**0.5

Of course, if you want to do this for geographical coordinates; I would recommend using the Inverse Vincenty Equation to calculate the distance over an ellipsoid. You can read more about this (as well as various methods for spherical distance calculations) in the distance page; and see a brief example on the handy hints page.

Heading

To work out the heading (direction) between the two locations, we need to use a little bit of Trigonometry. You might remember SOH CAH TOA from school, which is a simple pneumonic that helps you remember whether you need to use sin, cos or tan:

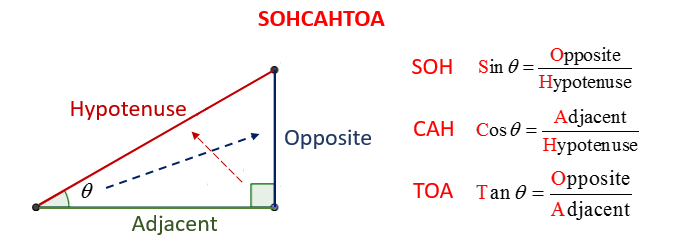
SOH CAH TOA is intended to help you work out which formula you need to solve a triangle. Each of the three formulas contains a combination of the length of two of the three sides of the triangle, and the angle \(\theta\). All that you have to do is select the one that includes both the information that you have access to and the information that you want.

For example, we are wanting to work out the direction between two points (those at either end of the Hypotenuse), which in the above diagram means working out the angle \(\theta\). If we are given the coordinates of the two points, then we know the length of the Adjacent side (\(\Delta x\), green in the above image) and the length of the Opposite side (\(\Delta y\), red in the above image), because we can simply subtract the coordinates to get the differences between them.

We therefore want to use the TOA equation, as this is the only one that includes the angle (\(\theta\)), the Opposite and the Adjacent:

Or, in more geographical terms:

Because we want to know \(\theta\), rather than \(Tan \theta\), we can rearrange this equation like this:

\(Tan^{-1}\) (Arc Tangent) is the opposite of \(Tan\) (Tangent), and its functionality is provided in the atan and atan2 functions of the Python math library. atan2is just a convenience function that allows you to pass in \(\Delta x\) and \(\Delta y\) as two separate arguments, and it handles the division for you.

Irritatingly for geographers, maths libraries in Python (and almost all other programming languages) calculate their results in radians rather than degrees, so you need to convert them using the degrees function in the Python math library:

degrees(atan2(location1[1] - location2[1], location1[0] - location2[0])

Another way in which atan2 might confuse a geographer is that it returns the angle measured from south on a scale of $-180$ to $180$, where we (as geographers) want the angle from north on a scale of $0$ to $360$. Fortunately - this is pretty easy to convert, we simply add $180$ to \(\theta\):

180 + degrees(atan2(location1[1] - location2[1], location1[0] - location2[0])

Finally, there is also a mathematical trick to play to ensure that the number you end up with is between 0 and 360. To achieve this, you need to add 360 to your result, and then calculate the modulus of your result and 360 using the modulo oparator (%). The Modulus is the remainder after you divide the numbers on each side of the operator, so, for example:

100 % 40 = 20

because 40 goes into 100 twice (80), leaving a remainder of 20. Here it is in context:

(180 + degrees(atan2(location1[1] - location2[1], location1[0] - location2[0])) + 360) % 360

To combine all of what we have discussed, then - the magic formula for calculating the heading between two points in degrees clockwise from north (which is what geographers expect…) is:

from math import degrees, atan2

def compute_heading(location1, location2):
    return (180 + degrees(atan2(location1[1] - location2[1], location1[0] - location2[0])) + 360) % 360

If you want to do this for geographical coordinates; I would recommend using the Inverse Vincenty Equation to calculate the forward and back azimuth (as well as distance) over an ellipsoid. You can read more about this in the handy hints page. Remember that the direction is presented as forward azimuth and back azimuth - as the direction relative to north changes throught the trajectory.

Point Offset

Another rather common problem in GIS that can be solved by Trigonometry is that of the offset: calculating a point at a given distance and direction from another point (e.g. what are the coordinates of a point 3km due east of my house).

Fortunately, this is also quite straightforward once you understand SOH CAH TOA. Let’s have another quick look at the image:

This time, we have the length of the Hypotenuse (red, the distance betwen the two points), and we need to calculate the location of the second point, which is simply:

Our task is then to calculate \(\Delta x\) (Adjacent, green) and \(\Delta y\) (Opposite, blue) and add them to \(x\) and \(y\) respectively!

Firstly, we need to decide which formula to use. For \(x\), we already have \(\theta\) and the length of the Hypotenuse (H) and we need the length of the Adjacent (A), so we need the CAH equation:

Or, in geographical terms:

Rearranging this to apply to our problem, we get:

So, to get the coordinates of \(x\):

As with atan2 above, the cos function in the Python math library expects angles to be in radians, so we must convert our heading from degrees to radians using the radians function from the Python math library.

from math import cos, radians, sin

def compute_offset(location, distance, direction):
    return (location[0] + cos(radians(direction)) * distance, 
      location[1] + sin(radians(direction)) * distance)

If you want to do this for geographical coordinates, I would recommend using the Forward Vincenty Equation to calculate the offset location over an ellipsoid. You can read more about this in the handy hints page.

Testing

Let’s see if it works:

Pick two random sets of coordinates (e.g. I tend to use 345678, 456789 and 445678, 556789) and print the distance and direction between them using your computeDistance and computeHeading functions.

Then calculate the offset point from your first set of coordinates, using the distance and heading values from the above calculation.

If all has gone to plan, the coordinates that you get back should be your second coordinate pair! Here it is in action:

from math import hypot, degrees, atan2, sin, cos, radians

def compute_distance(location1, location2):
    """
    Compute the distance between two locations using Pythagoras' Theorem
    """
    return hypot(location1[0] - location2[0], location1[1] - location2[1])

def compute_heading(location1, location2):
    """
    Compute the heading (direction) between two locations using trigonometry
    """
    return (180 + degrees(atan2(location1[1] - location2[1], location1[0] - location2[0])) + 360) % 360

def compute_offset(location, distance, direction):
    """
    Compute the location of a point at a given distance and direction from a specified location using trigonometry
    """
    return (location[0] + cos(radians(direction)) * distance, location[1] + sin(radians(direction)) * distance)


# set locations
location1 = (345678, 456789)
location2 = (445678, 556789)
print(f"\nlocations:\t\t\t{location1}, {location2}")

# calculate distance and heading
dist = compute_distance(location1, location2)
print(f"distance:\t\t\t{dist:.2f}")
head = compute_heading(location1, location2)
print(f"heading:\t\t\t{head}")

# calculate location 2 from location 1 and the distance and heading
new_location = compute_offset(location1, dist, head)
print(f"location 2 (re-calculated):\t{new_location}")
print(f"Expected result:\t\t{location2 == new_location}\n")

Which returns:

locations:                      (345678, 456789), (445678, 556789)
distance:                       141421.35
heading:                        45.0
location 2 (re-calculated):     (445678.0, 556789.0)
Expected result:                True